லில் ஸ்கைஸ் - தவழும் (சாதனை. பணக்கார குழந்தை) [தயாரிப்பு. வழங்கியவர் மெனோ பீட்ஸ்]
மங்காவின் 230 ஆம் அத்தியாயத்தில்,
இரண்டு முறை தன்னை ஆயிரக்கணக்கான மடங்கு பெருக்கிக்கொண்டார்
இரண்டு முறை தன்னை எத்தனை முறை நகலெடுக்க முடியும் என்பதற்கு வரம்பு உள்ளதா?
குறுகிய பதில் தத்துவார்த்த வரம்பு அல்ல, ஆனால் நன்கு வடிவமைக்கப்பட்ட வரம்புகள் காரணமாக நகைச்சுவையானது மிகைப்படுத்தப்படவில்லை.
அத்தியாயம் 230 இன் தொடக்கத்தில் அவரது 'இரட்டை' நகைச்சுவையின் விளக்கம் இது,
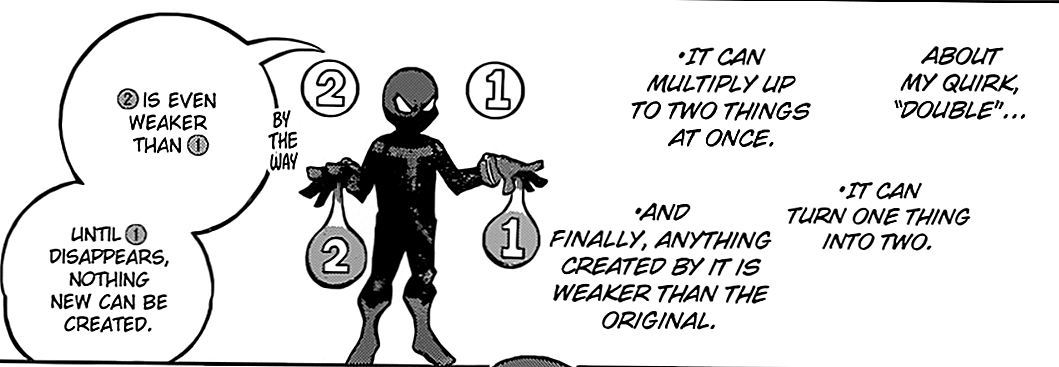
விக்கி பக்கத்தின்படி: (என்னுடையது வலியுறுத்தல்)
ஜினுக்கு ஒரே நேரத்தில் இரண்டு குளோன்களை மட்டுமே உருவாக்கும் வரம்பு உள்ளது. இருப்பினும், ஜின் தன்னை நகலெடுக்க முடியும் என்பதாலும், அவரது நகல்களுக்கும் டபுள் அணுகல் இருப்பதால், அவர் கோட்பாட்டளவில் தன்னைப் பற்றிய எல்லையற்ற பிரதிகளை உருவாக்கும் திறன் கொண்டது அவரது குளோன்கள் தங்களை மேலும் நகலெடுக்க அனுமதிப்பதன் மூலம். இது ஒரு பெரிய பணியை எளிதில் அல்லது பல சிறிய பணிகளை ஒரே நேரத்தில் உணர ஜினுக்கு மனிதவளத்தை அளிக்கிறது, அவருடைய குளோன்கள் அவருடன் ஒத்துழைக்கின்றன. இறந்தவர்களைக் கூட இரட்டிப்பாக்க முடியும் என்று டோமொயாசு சிகாசோகு கூறுகிறார்.
நான் பார்க்கும் விஷயத்திலிருந்து 2 வரம்புகள் உள்ளன:
குளோன்களின் ஆயுள். உடைந்த எலும்புக்கு சமமான காயம் ஒரு குளோனைக் கரைக்கும் என்று இரண்டு முறை குறிப்பிடுகிறது, அதே நேரத்தில் இரண்டாவது நகல் பொதுவாக பலவீனமாக இருக்கும்.
குளோன்கள் தன்னாட்சி கொண்டவை. அவரால் அவற்றை உண்மையில் கட்டுப்படுத்த முடியாது, அவற்றை உருவாக்கி அவர்களின் இறப்புகளைக் கண்டறிய மட்டுமே முடியும். இது சாத்தியமான தன்னை விட சக்திவாய்ந்த எந்த ஹீரோக்கள் அல்லது வில்லன்களையும் கூட குளோன் செய்வதிலிருந்து தடுக்கிறது. எல்லாவற்றிற்கும் மேலாக, அவர் தனது சொந்த குளோன்களால் கிட்டத்தட்ட அவரைக் கொன்றதால் ஆழ்ந்த அதிர்ச்சியடைந்தார், தற்போதைய முன்னேற்றங்களுக்குப் பிறகும், அவர் "எல்லையற்ற இரட்டையர்" நகர்வை கடைசி முயற்சியாக தவிர வேறு எதையும் பயன்படுத்துவார் என்று நான் சந்தேகிக்கிறேன்.
ஒரு சுவாரஸ்யமான அவதானிப்பு, அதற்கான எந்த உறுதிப்பாட்டையும் என்னால் கண்டுபிடிக்க முடியவில்லை. எல்லையற்ற வரம்பு அவரது குளோன்கள் அனைத்தும் (குளோன்களால் உருவாக்கப்பட்டவை கூட) அசலுக்கு விகிதாசாரமாக இருக்கும் என்பதைக் குறிக்கிறது. திறனைப் பயன்படுத்தும் குளோனை அடிப்படையாகக் கொண்டதாக இருக்கும் என்று நான் ஆரம்பத்தில் நினைத்தேன், இந்நிலையில் கூட்டு அபராதங்கள் ஒரு கணித வரம்பைக் கட்டாயப்படுத்தும், அதன் பிறகு குளோன்கள் கொல்ல மிகவும் எளிதானவை.







